Pressure drop reduction and heat transfer deterioration in circular pipe flow, and the PIV method
In the transportation of slush hydrogen or slush nitrogen via pipeline
for use as the refrigerant for high-temperature superconducting (HTS) power
transmissions and equipments, it is important to consider pressure drop
due to straight pipes, as well as flow restrictions such as valves, converging-diverging
pipes, and orifices. Such pipelines also often make use of corrugated pipes
to absorb the cryogenic contraction (stainless-steel pipe contracts by
approximately 3 mm per 1 m). Increased pressure drop during slush fluid
transport requires greater pump power, thus reducing the overall performance
of the transport system.
When slush nitrogen is to be used as the refrigerant for HTS power transmission,
heat generation can be anticipated due to superconductor quench, making
it important to also consider pressure drop of slush nitrogen during heat
transfer, together with forced convection heat transfer to slush nitrogen.
Flow and heat transfer experiments were performed with respect to slush
nitrogen flow in a horizontal heat transfer pipe. From the experimental
results, we firstly reported in the world that the pressure drop reduction and heat
transfer deterioration (i.e., pressure drop and heat transfer coefficient
for slush nitrogen are less than those of liquid nitrogen) emerged simultaneously
during pipe flow, and the mechanisms involved in pressure drop reduction
and heat transfer deterioration have been elucidated [20, 21].
The simultaneous occurrence of the pressure drop reduction and heat transfer
deterioration shows that "the Reynolds' analogy" holds in the case of slush nitrogen flow, too.
In addition to the quantitative determination of pressure drop reduction
and heat transfer deterioration, We have also reported on the visualization
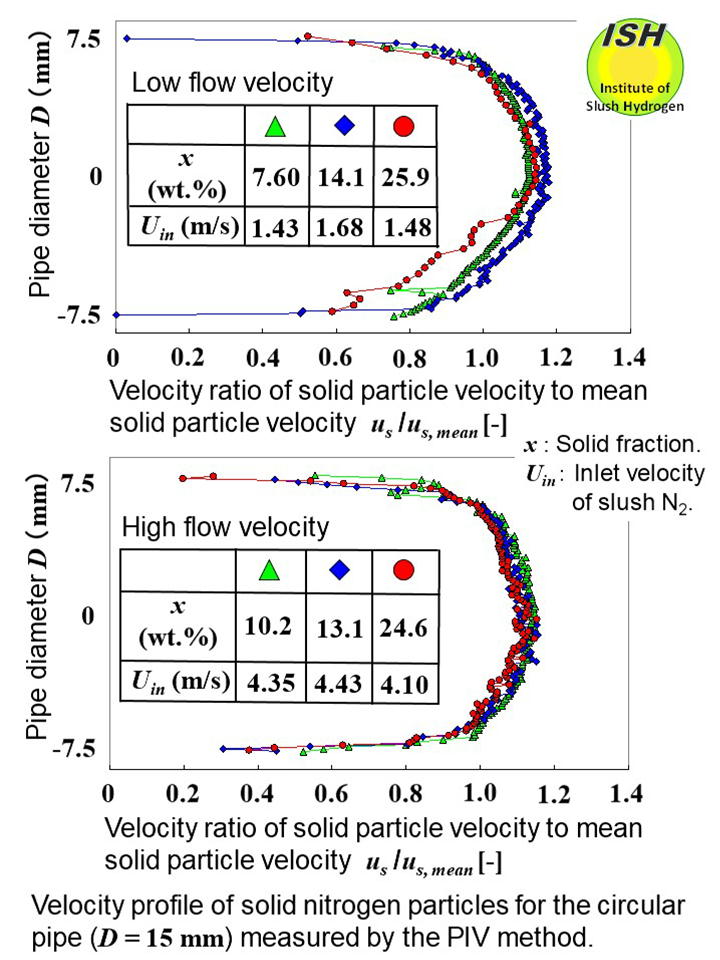
of solid particle behavior by means of a high-speed video camera and flow
velocity distribution of solid particles measured using the PIV method*
as shown in the figure below, as well as the elucidation of the reduction of the reduction and deterioration
mechanisms through flow analysis, employing a numerical analysis code (SLUSH-3D)
that we developed.
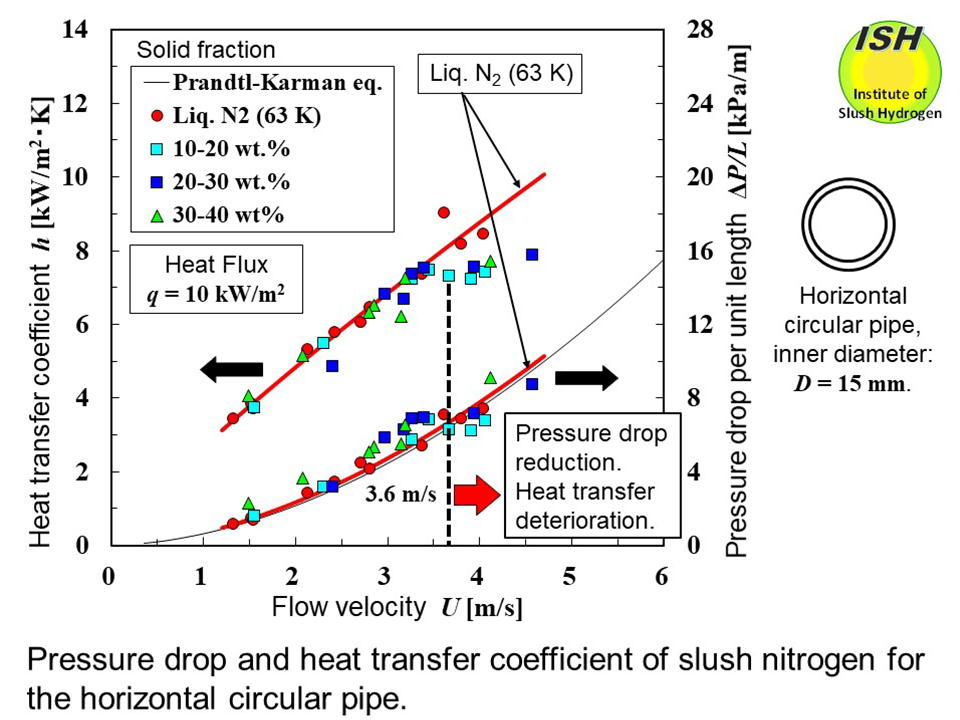
From our previous research results, it was found that in the pseudo-homogeneous
flow of slush nitrogen (63 K) in horizontal circular pipes having diameters
of 10 mm and 15 mm, at flow velocities of over 2.0 m/s and over 3.6 m/s,
the maximum reductions in pressure drop were 25% and 23%, respectively,
in comparison with liquid nitrogen (63 K). Also, we have reported that
at heat flux of 10 kW/m2, the maximum pressure drop reductions were 23% and 17%, while at the same
time the maximum deteriorations in heat transfer coefficient were 27% and
20% as shown in the above figure [20, 21].
The mechanism involved in pressure drop reduction and heat transfer deterioration
is summarized as follows:
When pipe flow velocity increases and heterogeneous flow changes to pseudo-homogeneous
flow in the case of heated or unheated flow, such that the solid particles
move towards the center region of the pipe (refer to the figure in "Numerical
analysis of slush flow by SLUSH-3D"), interference decreases between
the solid particles and the pipe wall. Here, the pipe center region refers
to the region inside the pipe excluding the thin liquid layer near the
pipe wall in which there are few solid particles.
This movement of solid particles to the center results in a grouping of
particles that suppresses the development of turbulence at the pipe wall,
thus resulting in pressure drop reduction. Although heat transfer takes place near the pipe wall where the liquid
layer contains few solid particles, the comparative lack of turbulence in this region means that the heated
liquid near the wall is prevented from dispersing towards the pipe center,
causing heat transfer deterioration.
When slush fluid is subjected to pumped transport over a long distance
in combination with superconducting electrical power transmission, pressure
drop reduction and heat transfer deterioration are extremely important
from the standpoint of design data required to reduce the required power
for pumps and to prevent quench propagation.
In other research on pressure drop reduction in slush fluid, only one
experimental result obtained by Sindt et al. has been reported indicating
the occurrence of this phenomenon in slush hydrogen flowing in a circular
pipe having an inner diameter of 16.6 mm [32]. Only the pressure drop of
slush hydrogen was measured, and there was no attempt to explain the reduction
or to consider the heat transfer properties.
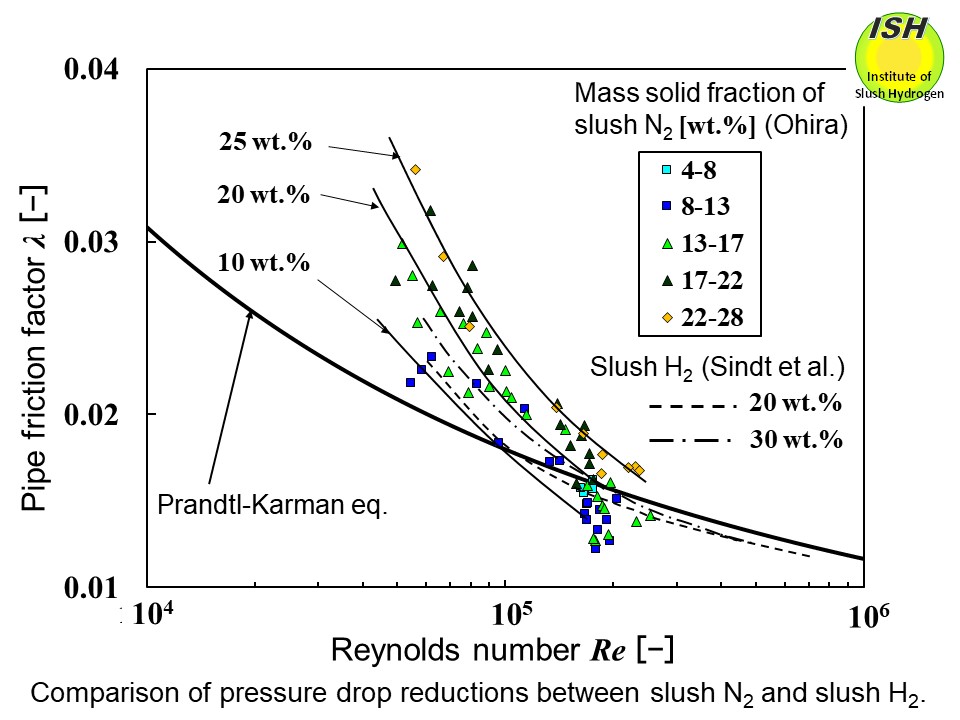
The relationship between the Reynolds number and the pipe friction factor
for slush nitrogen flowing in a circular pipe with an inner diameter of
15 mm and slush hydrogen is shown in the figure below. The solid line indicates the Prandtl-Karman eq. for a single-phase liquid.
Pressure drop reductions for slush hydrogen and slush nitrogen appear
for the Reynolds (Re) numbers of 1.0×105 and above, and as the solid fraction increases, the Re number at the onset of pressure drop reduction becomes greater.
However, the velocity at which pressure drop reduction initiated with
respect to slush hydrogen for an inner diameter of 16.6 mm was lower than
that in the case of slush nitrogen for a 15 mm diameter pipe (nearly the
same diameter) at identical solid fractions. That is, as indicated in the
figure, for a solid fraction of 20 wt.%, the Re number at which the reduction initiates is 1.0×105 for slush hydrogen and 1.5×105 for slush nitrogen. Since the kinetic viscosities are about the same for
both, the reduction initiates at lower flow velocity in the case of slush hydrogen. The solid-liquid density ratio is lower for slush hydrogen (1.12 vs. 1.18
for slush nitrogen), and, as the viscosity of liquid hydrogen is 1/11 that
of liquid nitrogen, pseudo-homogeneous flow occurs at lower flow velocity.
These results suggest that the pressure drop reduction effect is manifested
in pseudo-homogeneous flow [20] (refer to the figure in "Numerical analysis of slush flow by
SLUSH-3D").
Taking unheated pressure drop test results for circular pipe, we applied
the least squares approximation method to obtain a correlation equation
between the slush Reynolds number ReSL using the apparent viscosity μSL = μL [1- (x/0.6)]-1.8 [33], and the pipe friction factor λ. Here, μL is liquid nitrogen viscosity. The correlation equation, as shown in the figure below, can accurately estimate the pipe friction factor from the flow velocity
and volumetric solid fraction x (not mass solid fraction) [20].
The correlation equation takes pressure drop reduction into account, and
will be effective for design work when estimating required pumping power
for the transport of slush nitrogen.
* PIV method: The velocity of solid particles is directly measured using
the Particle Image Velocimetry method.