Pressure drop reduction and heat transfer deterioration in triangular and square pipe flows

　In the transportation of slush hydrogen or slush nitrogen via pipeline for use as the refrigerant for high-temperature superconducting (HTS) power transmission and equipment, the flow and heat transfer characteristics of slush fluids are important in pipe flow.
　The occurrence of pressure drop reduction in the high-velocity flow means that reduced pumping power can be anticipated in pipeline transport. The use of pipes with various cross-sectional shapes can be expected for both transport piping and superconducting power transmission refrigerant piping.
　In comparison to circular pipe having the same hydraulic diameter, triangular pipe has greater heat transfer surface area and superior integration, and is therefore also used in applications such as the plate-fin type heat exchanger.

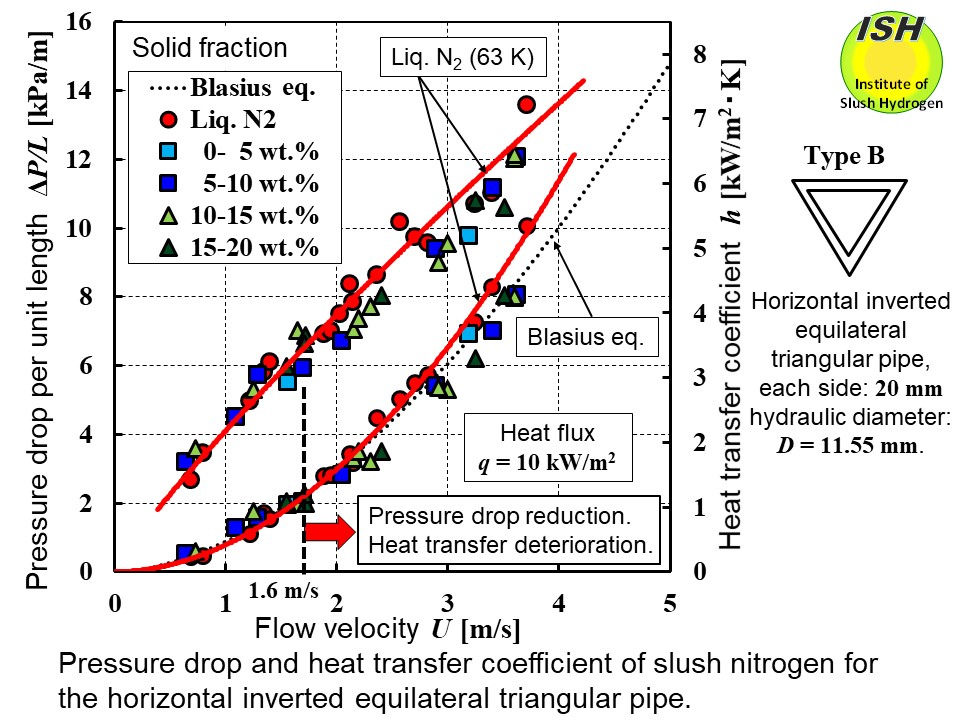
　In the case of an equilateral horizontal triangular pipe with each side of 20 mm (hydraulic diameter D = 11.55 mm) under the conditions of three different cross-sectional orientations (Types A, B, and C) and heat fluxes (0, 10, and 20 kW/m²), experimental results of slush nitrogen obtained for Type B at heat flux of 10 kW/m² is shown in the above figure.
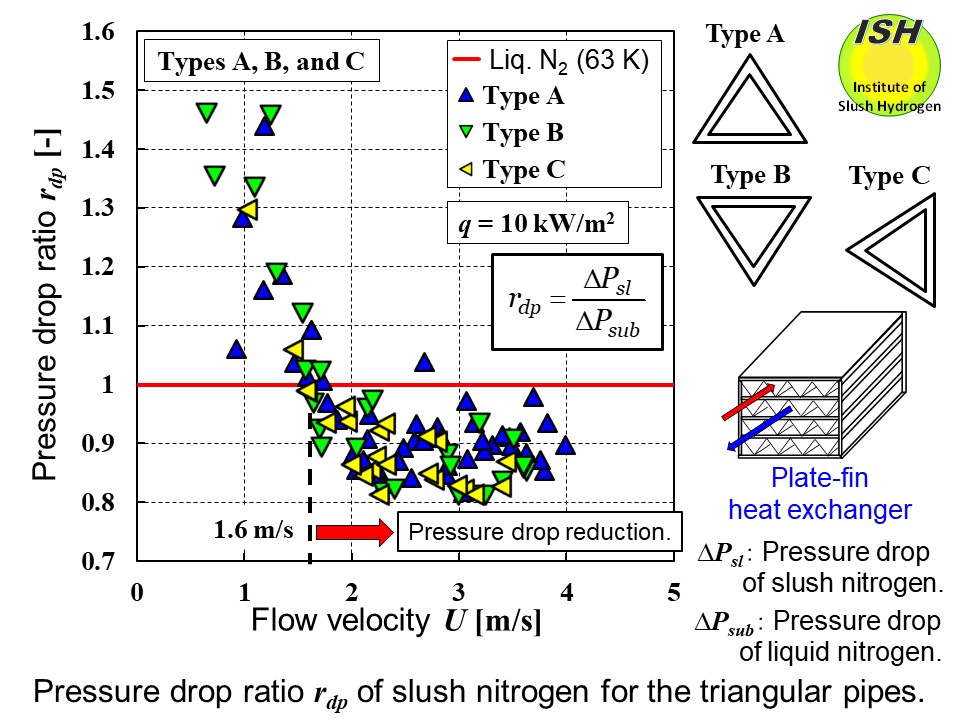
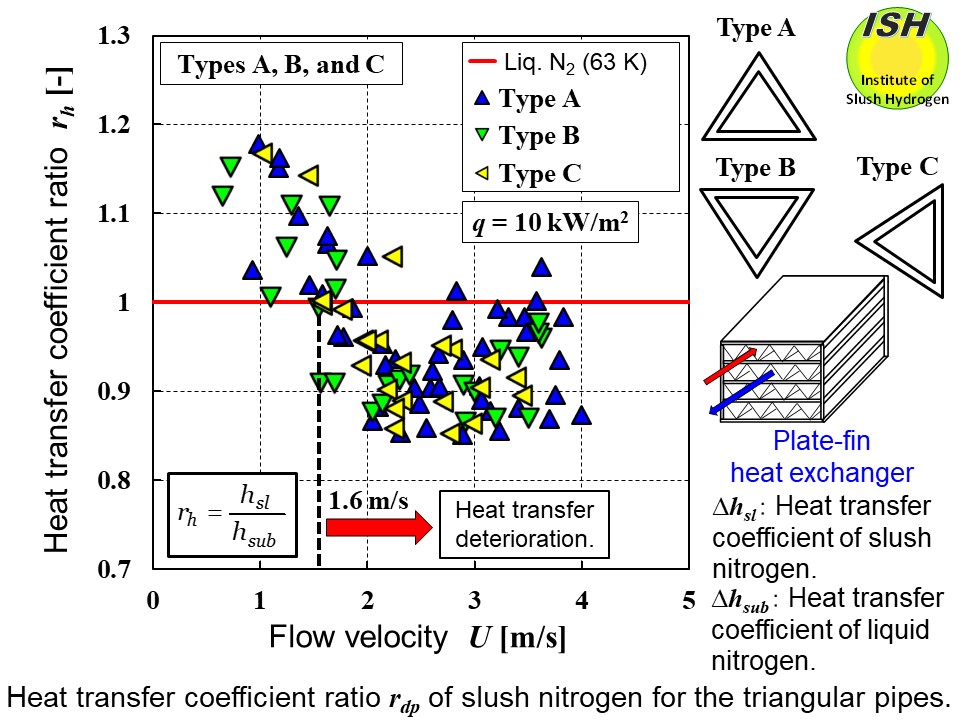
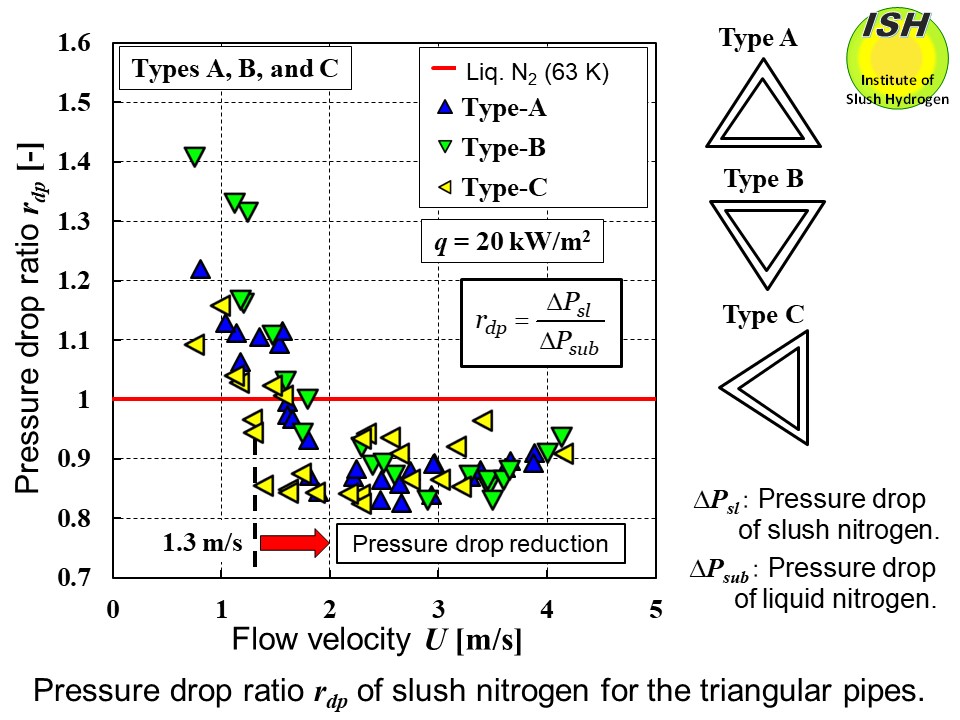
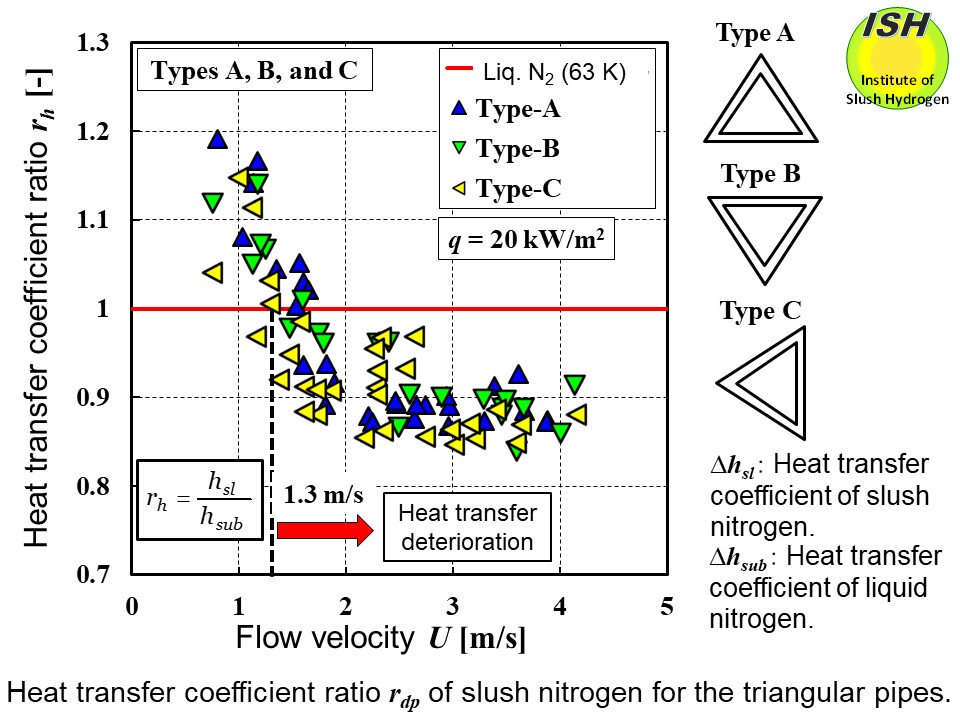
　For Types A, B, and C, the relationships for slush nitrogen between the flow velocity and the pressure drop ratio, and between the flow velocity and the heat transfer ratio are illustrated in the figures below at heat fluxes of 10 kW/m² and 20 kW/m². Pressure drop ratio is the ratio of slush nitrogen pressure drop to liquid nitrogen pressure drop, and heat transfer ratio is the ratio of the heat transfer coefficient for slush nitrogen to that for liquid nitrogen.
　The simultaneous occurrence of the pressure drop reduction and heat transfer deterioration shows that "the Reynolds' analogy" holds in the case of slush nitrogen flow, too. About the mechanism involved in pressure drop reduction and heat transfer deterioration, refer to the page "Circular pipe flow and PIV".
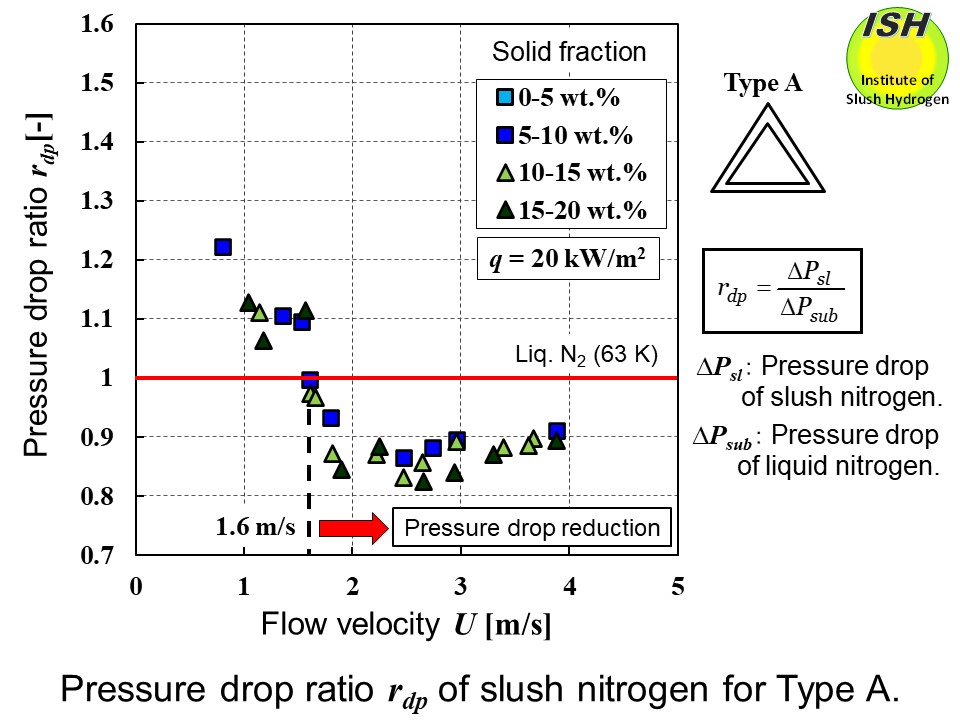
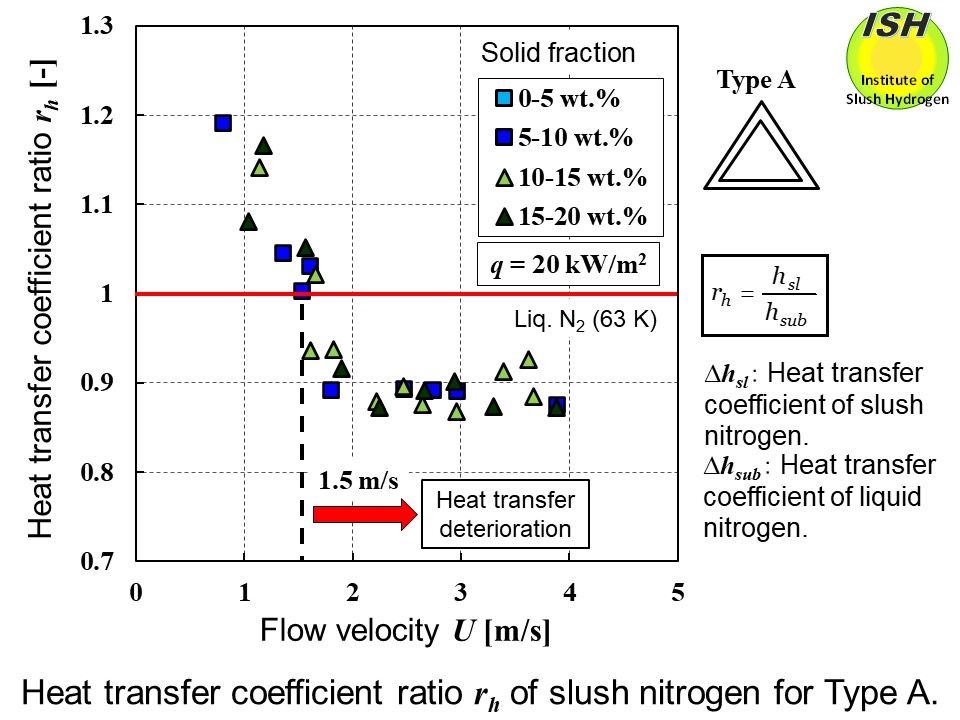
　Since all of the experimental data with the different solid fraction are summarized in the figure for each ratio, variations shown in the figure are largely due to the difference in solid fraction, not to the measurement error. The difference in solid fraction of pressure drop ratio and heat transfer ratio for Type A at heat flux of 20 kW/m² is shown in the figures below for reference.

　For Types A, B, and C, the pressure drop reduction was a maximum of 16-19% in comparison with liquid nitrogen at flow velocities exceeding 1.3-1.8 m/s, regardless of heating. Heat transfer deterioration was seen at flow velocities exceeding 1.2-1.8 m/s for a maximum of 13-16% [22, 24].

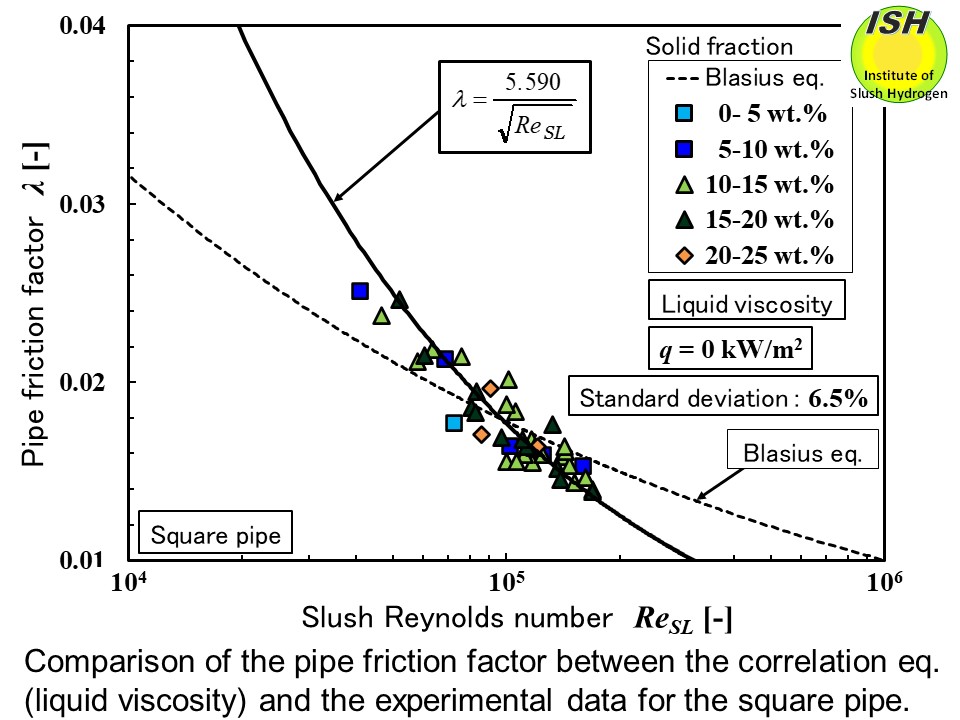
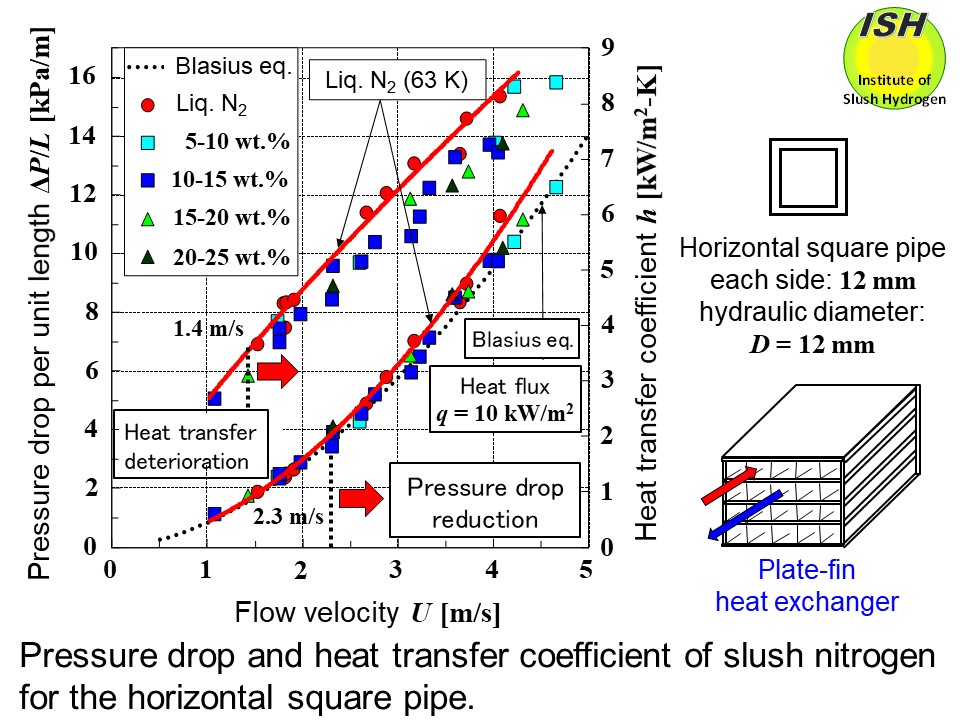
　In the case of a horizontal square pipe　with each sides of 12 mm, at a flow velocity of over 2.5 m/s, the reduction in pressure drop was a maximum of 12% as compared to liquid nitrogen; at heat flux of 10 kW/m²as shown inthe figure below, the maximum pressure drop reduction was 12% at a flow velocity of over 2.3 m/s, while at the same time heat transfer coefficient deterioration was a maximum of 16% at a flow velocity of over 1.4 m/s [23, 24].

　The simultaneous occurrence of the pressure drop reduction and heat transfer deterioration, i. e. "the Reynolds' analogy" holds in the case of triangular and square pipe flows, too.

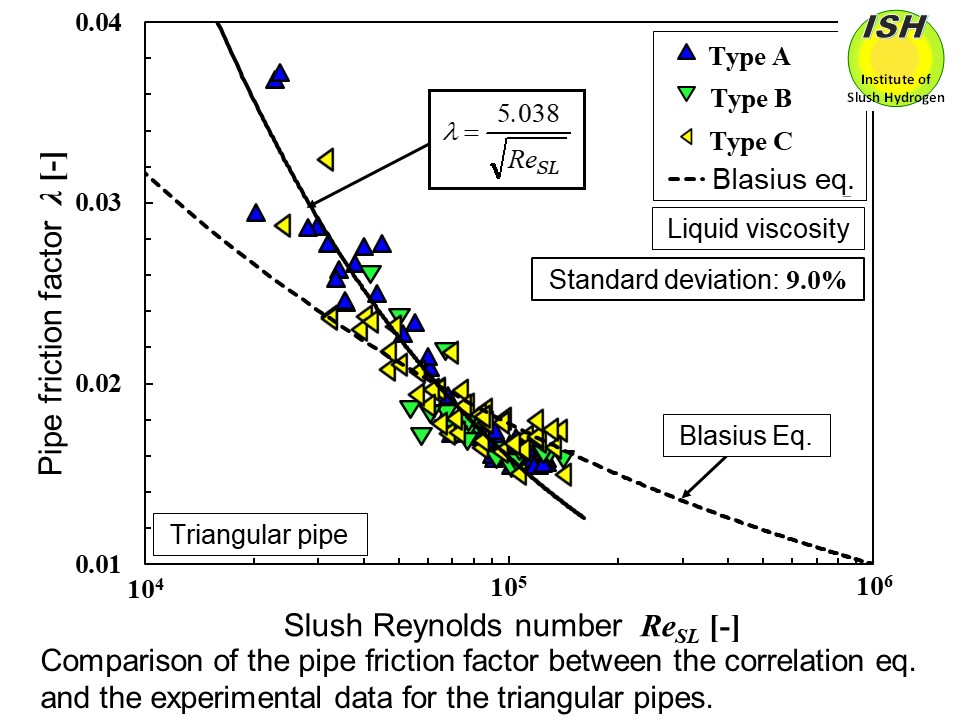
　Taking unheated pressure drop test results for an equilateral horizontal triangular pipe, we applied the least squares approximation method to obtain a correlation equation between the slush Reynolds number Re_SL using the liquid nitrogen viscosity μ_L, and the pipe friction factor λ. For triangular and square pipes, the utilization of the liquid nitrogen viscosity as the apparent viscosity for the slush Reynolds number enables the most accurate estimation of the pipe friction factor because the pressure drop reduction in triangular and square pipes is smaller than for circular pipe. As shown in two figures below, the correlation equation for the unheated triangular and square pipes can accurately estimate the pipe friction factor from the flow velocity and volumetric solid fraction x (not mass solid fraction) [24].

　These correlation equations take pressure drop reduction into account, and will be effective for design work when estimating required pumping power for the transport of slush nitrogen.